Математична модель штучного нейрона і нейронної мережі

Схематично математичну модель штучного нерона можна описати таким чином.

Штучним нейроном із $n$ входами називається функція $y: \mathbb{R}^n \to \mathbb{R}$, яка відображає вхідний вектор $X=(x_1,x_2, \ldots, x_n) \in \mathbb{R}^n$ в число $y(X)$ за правилом $$ y(X)=f( x_1 w_1+x_2 w_2+\cdots+x_n w_n +b)=f\left( \sum_{i=1}^n x_i w_i +b \right). $$ У векторній формі ця функція може бути записана так $$ y(X)=f( W X +b), $$ де $WX$ -- скалярний добуток векторів $W$ i $X$. Схематично, за аналогією із біологічним нейроном, штучний нейрон виглядає так (індекси зміщені)

Введемо спеціальну термінологію, яка використовується в штучних нейронних мережах

• векторний простір $\mathbb{R}^n$ називається простором ознак
• змінні $x_i$ називаються входами (inputs) нейрона
• параметри $w_i$ називаються вагами (weights) нейрона
• параметр $b$ називається зсувом (bias)
• значення функції $y(X)$ називається виходом, відгуком (output) нейрона
• функція $f:\mathbb{R} \to \mathbb{R}$ називається функцією активації (збудження) (аctivation function) нейрона
• Гіперплощина $x_1 w_1+x_2 w_2+\cdots+x_n w_n +b=0$ в просторі ознак $\mathbb{R}^n$ називається розділюючою гіперплощиною нейрона.

Як правило, функцію активації $f$ підбирають так, щоб множина значень була інтервалом $ [0,1]$ або $[-1,1]$, $[0,\infty].$ Найчастіше використовуються такі функції

• Сигмоїдна функція активації $$ \sigma(x)=\frac{1}{1+e^{-x}}, $$
  
• {ReLU (rectified linear unit):}Функція $f(x)=\max(0,x)$
• Функція $f(x)={\rm sign}(x)=\begin{cases} 1, x>0,\\ 0, x \leq 0. \end{cases}$
  

Основна обчислювальна властивість нейрона полягає в тому, що він визначає деяку гіперплощину в просторі ознак, яка розділяє цей простір на дві частини. Тобто, для всіх точок з одного боку гіперплощини нейрон, як функція приймає одне значення, а для інших точок інше. Наприклад для функції ${\rm sign}(x)$ цими значеннями будуть $-1$ i $0$. Ця обставина дозволяє використати штучний нейрон для таких простих задач бінарної класифікації, для яких дві множини ознак можна відокремити розділяючою гіперплощиною.

Визначення коефіцієнтів цієї розділяючої гіперплощини називається навчанням нейрона. Штучний нейрон називається навченим для деякої бінарної задачі класифікації, якщо його розділяюча гіперплощина відокремлює два класи у просторі ознак даної задачі. Зрозуміло, що для даної задачі може існувати багато розділяючих гіперплощин, тому навчити нейрон можна, як правило, неоднозначно.

Проте, для багатьох реальних задач, одного нейрона недостатньо для проведення класифікації, тому потрібно задіяти більшу кількість нейронів, які об'єднують в шари, а шари в в нейронні мережі різної архітектури.

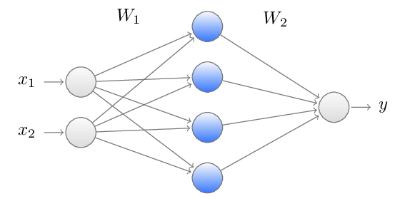
Ось приклад нейронної мережі із вхідним шаром (input layer) із двох нейронів, одним прихованим шаром (hidden layer) із чотирьох нейронів і вихідним шаром (output layer) із одного нейрона.

Вагові коефіцієнти чотирьох нейронів прихованого шару утворюють $4 \times 2$ матрицю $W_1:$ $$ W_1=\begin{pmatrix} w_{1,1} w_{1,2} \\ w_{2,1} w_{2,2} \\ w_{3,1} w_{3,2} \\ w_{4,1} w_{4,2}\end{pmatrix} $$ та вектор-зсувів $B_1$ $$ B_1=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \\ b_4\end{pmatrix} $$ Як функція, на вході цей шар отримує двовимірний вектор-стовпчик $X^\top =(x_1,x_2) \in \mathbb{R}^2,$ а на виході отримуємо чотиривимірний вектор стовпчик, який в матричному вигляді записується так $$ f_1\left(W_1 x+B_1 \right) \in \mathbb{R}^4. $$ Тут $f_1$ функція активації, яку ми будемо вважати однаковою для кожного нейрону цього шару, і яка діє поелементно на кожну компоненту вектора.

Далі отриманий стовпчик передається останньому шару з $4 \times 1 $ матрицею $W_2$, функцією активації $f_2$ i вектором зсувів $B_2$, у нашому випадку, це просто число, оскільки в останньому шарі тільки один нейрон. В результаті, числова функція $y:\mathbb{R}^4 \to\mathbb{R}$, яку реалізує ця нейронна мережа має вигляд $$ y(X)=f_2\left(W_2 f_1\left(W_1 x+B_1 \right)+B_2\right), $$ і залежить від 17 параметрів.

Нейронна мережа з такою архітектурою називається нейронною мережею прямого поширення (Feedforward neural network).

Багатошарова нейронна мережа прямого поширення (Multilayer feedforward neural network) із $n$ шарами, є послідовною композицією функцій шарів і реалізовує таку функцію $$ y(X)=f_n\left( W_n\left( \ldots f_2\left( W_2 f_1\left(W_1 x+B_1 \right)+B_2\right)\ldots \right) +B_n \right), $$ тут $W_i, B_i, f_i$ відповідні матриці вагових коефіцієнтів, вектори зсуву та функції активації для кожного шару. Однією із найважливіших властивостей цієї функції, яка лежить в основі ефективності нейронних мереж, є те що ця функція не має оберненої.

Багатошарові нейронні мережі різної архітектури, дозволяють вирішувати задачі класифікації, особливо вони є ефективними для розпізнавання образів.