Фільтрація в частотній області

Двовимірний фільтр низьких частот, який пропускає без загасання всі частотні складові всередині кола радіусом $D_0$ з центром в початку координат і ''обрізає'' всi частотні складові поза цим колом, називається ідеальним фільтром низьких частот (ідеальний ФНЧ) визначається наступною передаточною функцією $$ H(u,v)=\begin{cases} 1, \text{ якщо $D(u,v)\leq d $},\\ 0, \text{ якщо $D(u,v) \geq d $}, \end{cases} $$ де $D(u,v)$ -- відстань від точки $(u,v)$ в частотній області до початку координат.

Передавальна функція фільтру низьких частот Баттерворта порядку $n$ з частотою зрізу на відстані $D_0$ від початку координат задається формулою $$ H(u,v)=\frac{1}{1+\left( \frac{D(u,v)}{D_0} \right)^n} $$

Гаусівський фільтр низьких частот задається передавальною функцією $$ H(u,v)=e^{\frac{D(u,v)^2}{2 D_0^2}}. $$

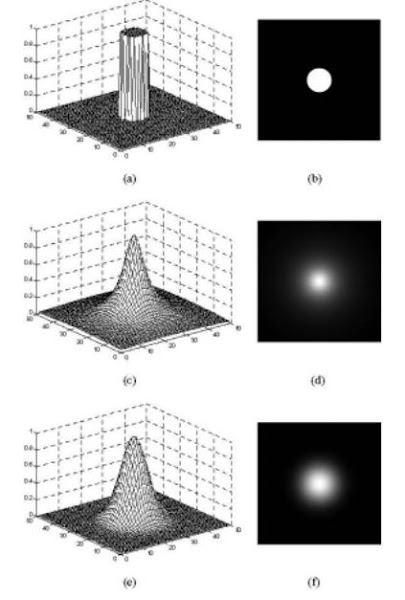
(a)-(b) - Ідеальний фільтр, (c(-(d) -- фільтр Баттерворта та фільтр Гауса (e)-(f)

Також популярні смугові фільтри які вирізають конкретний діапазон частот:

або фільтри які вирізають конкретні частотні області.

(а) Газетне зображення, видно муаровий малюнок. (б) Спектр. (c) Перетворення Фур'є, помножене на смуговий фільтр Баттерворта (d) Відфільтроване зображення.

Основною властивістю, яка визначає важливість перетворення Фур'є в обробці зображень є його проста дія на згортку функцій, яка перетворюється на простий добуток функцій-образів.

Етапи фільтрації зображення в частотній області:

Крок 1: Застосувати перетворення Фур'є, щоб перетворити зображення у 2D-частотну область.

Крок 2: Застосувати відповідний фільтр частотної області.

Крок 3: Застосувати обернене перетворення Фур'є, щоб перетворити зображення в просторову область.